

Value at risk (VaR) is a risk measure that has been widely implemented by financial institutions. The VaR of a portfolio can be computed by two approaches: first, by considering the distribution of asset price changes of the whole portfolio and then compute the portfolio VaR as a quantile of this distribution; second, by considering the distribution of price changes of each asset, then compute the VaR for each asset and finally compute the portfolio VaR by using an aggregation formula such as the formula developed by JP Morgan in RiskMetrics. If asset price changes are distributed according to a Gaussian distribution, then the same number should be found for the correlation coefficient.
The contribution of this paper is to test if the correlation among asset price changes implied from VaR calculation is constant. The idea is to use VaR models in a reverse way as done with option pricing models to get the implied volatility of asset prices. The correlation implied from VaR should be independent of the type of position (long or short) and of the probability used to compute the VaR. It should be simply equal to the classical Pearson correlation coefficient. Whether this proposition holds true is empirically tested in the paper.
The figure below represents the correlation implied from daily VaR of long and short positions on an equally-weighted portfolio composed of the S&P 500 and FTSE 100 indexes over the time-period from January 1, 1995 to December 31, 2003. VaR is computed from different average waiting time-periods (or equivalently probability levels) representing the average time-period needed to observe a random variable lower (or higher) than a given level.
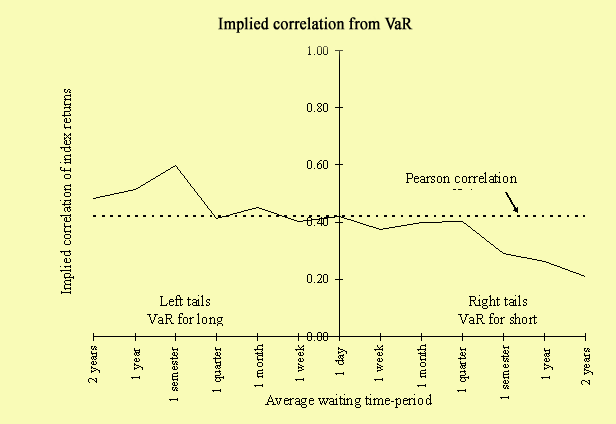
The main result of this paper is that the implied correlation tends to depend on the type of position (long or short) and on the probability level used to compute the VaR. The implied correlation for long positions is higher than the Pearson correlation coefficient while it is systematically lower for short positions. The implied correlation for long and short positions tends to diverge as the probability level used to compute the VaR increases (that is when we look further in the distribution tails).
 Return to the publication list
Return to the publication list
Extreme correlation in international equity markets
Is the correlation in international equity returns constant: 1960-1990 ?
From VaR to stress testing : the extreme value approach