

This article received the award of the Chicago Board of Trade for the research on derivative products.
Risk is one of the most important factors in the management of financial assets. The efficiency of risk management methods such as portfolio insurance is largely undermined during periods of extreme volatility like stock market booms and crashes. The accuracy of portfolio insurance critically depends on the process followed by the market price: the possibility of gap openings, jump movements and unexpected changes in volatility may undermine the strategy during periods of market stress. Moreover, portfolio insurance may be liable to have a destabilizing effect on the market during these periods. In any event, such a dynamic hedging technique has been less used by market participants since the last stock market crash of October 1987.
The contribution of this article is to introduce a new type of financial derivatives called boom and crash options in order to improve the performance of portfolio insurance techniques, especially during periods of market stress. The purpose of crash options for example is to protect the value of a long position against a sharp, large decline in market prices. Portfolio managers could use crash options to limit their extreme downside risk. Crash options complete the spectrum of existing options as they focus on extreme price changes during a short period. In their conception crash options are relatively close to lookback options whose payoff depends on the maximal or minimal price reached by the expiration date. Although lookback options deal with the difference between the price at the expiration date and its maximum or minimum reached during their life-time, crash options deal with the minimal price changes computed over a short period of time.
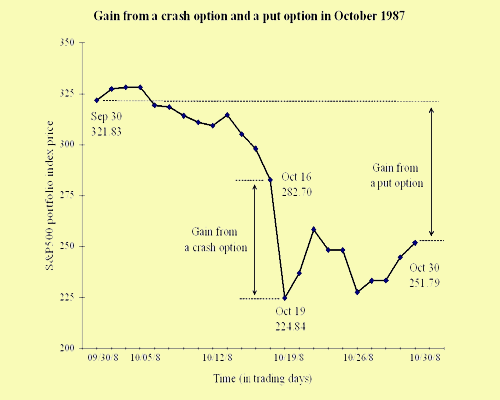
The main result of the paper is to price and derive a pricing strategy for boom and crash options. Two types of market are considered : a market with few extreme price movements (returns are drawn from a thin-tailed distribution such as the Gaussian distribution) and a market with many extreme price movements (returns are drawn from a fat-tailed distribution).
 Return to the publication list
Return to the publication list
The asymptotic distribution of extreme stock market returns
Optimal margin level in futures markets