Quels sont les principaux risques de marché auxquels sont confrontés les banques ? Certains ont-ils pris récemment une plus grande importance ? Quels sont les moyens à la disposition des banques pour mesurer au mieux ces risques ? Quelles sont les insuffisances mais aussi l'intérêt de la VaR en termes de mesure du risque de marché ? Telles sont les questions abordées dans cet article.
De manière générale, le risque de marché est défini comme limpact de la variation de certaines variables de marché (comme les prix dactifs tels que les actions ou les matières premières, les taux dintérêt et les taux de change) sur la valeur des positions des banques. Suite à la réglementation sur la mesure et le suivi des risques de marché datant du milieu des années 1990, certaines banques ont mis en place des modèles internes permettant dappréhender ces risques. Ces modèles reposent sur le concept de la value at risk (VaR) et utilisent des méthodes statistiques. Par définition, la VaR dune position de marché correspond à la perte maximale de cette position sur une période donnée et pour un seuil de confiance donné. Pour illustrer ce concept, une VaR de 1 M signifie que, dans 99% des cas, la position ne perdra pas plus de 1 M, et de façon équivalente que, dans 1% des cas seulement, la position perdra plus de 1 M. En pratique, la VaR est estimée par différentes méthodes statistiques : la méthode historique, la méthode paramétrique et la méthode de simulation de Monte Carlo.
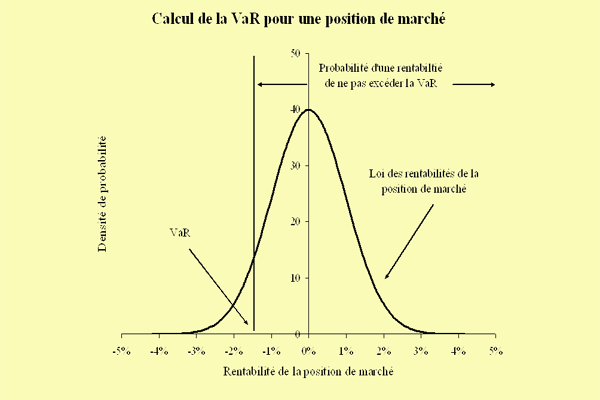
La VaR, en tant que modélisation de la réalité, ne décrit pas forcément parfaitement cette réalité. Premièrement, comme toute modélisation, la VaR est soumise au risque de modèle. Pour la méthode paramétrique par exemple, la VaR dépend du choix de la loi statistique. La loi normale qui est souvent utilisée tend à sous-estimer les événements extrêmes comme les krachs boursiers. Un tel modèle entraînera donc une sous-estimation de la VaR. Deuxièmement, la VaR nest pas toujours une statistique exhaustive pour décrire les risques de marché. En particulier, elle ne renseigne pas sur le montant des pertes au-delà de la VaR. Par exemple, pour une VaR de 1M calculée avec un seuil de confiance de 99%, combien la banque perdra dans le 1% des cas qui correspondent au dépassement de la VaR? 1 M, 10 M ou 100 M ?
Application de la théorie des valeurs extrêmes aux marchés financiers
From VaR to stress testing : the extreme value approach
Retour à la liste des publications
Conseil en gestion des risques
Glossaire de termes financiers
