The traditional approach to VaR consists in studying the distribution of the variations of position value over a given period. The main methods that are the historical method, the method of Monte Carlo simulation, and the method of variance-covariance based on the Gaussian distribution are often regarded as imperfect. In particular, these methods tend to underestimate the extreme events observed on the markets.
The computation of capital requirement for financial institutions should be considered as an extreme value problem. Extraordinary events such as the stock market crash of October 1987, the breakdown of the European Monetary System in September 1992, the turmoil in the bond market in February 1994 and the recent crisis in emerging markets are a central issue in finance and particularly in risk management and financial regulation. The performance of a financial institution over a year is often the result of a few exceptional trading days as most of the other days contribute only marginally to the bottom line. Regulators are also interested in market conditions during a crisis because they are concerned with the protection of the financial system against catastrophic events which can be a source of systemic risk.
The contribution of this article is to present a new approach to VaR: the extreme value approach. Based on extreme value theory, it considers the distribution of extreme returns instead of the distribution of all returns: market corrections during ordinary periods, and also market crashes during extraordinary periods. Applied to finance, extreme price movements can thus be observed during usual periods corresponding to the normal functioning of financial markets and during highly volatile periods corresponding to financial crises. An approach based on extreme values then covers market conditions ranging from the usual environment considered by the existing VaR methods to the financial crises which are the focus of stress testing.
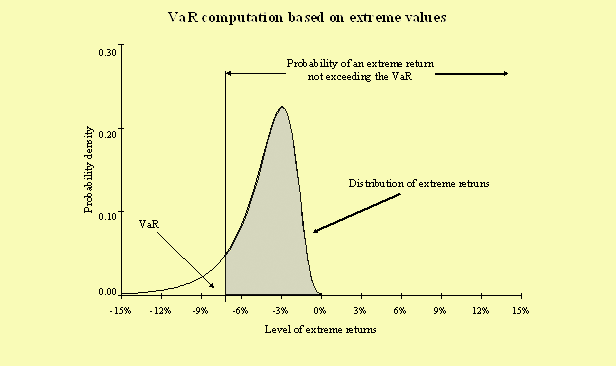
As shown in the figure above, for a given probability, the VaR is obtained as the quantile of the distribution of extreme returns. In practice, this distribution estimated from a long time-period is often a Fréchet distribution.
Extreme correlation in international equity markets
The asymptotic distribution of extreme stock market returns
From VaR to stress testing : the extreme value approach
Retour à la liste des publications
Conseil en gestion des risques
Glossaire de termes financiers
