Extreme events in financial markets such as stock market crashes, bond market collapses and foreign exchange crises are of great importance for individuals and institutions. These rare but important events are however difficult to understand for academics and practitioners as well. A few years after the October 1987 crash, we are still wondering what could cause a 20% drop of the U.S. stock market and its propagation other markets. Up to now, extreme events haven't been dealt in a rigorous scientific manner, econometricians considering such observations as outliers.
The contribution of this article is to quantify the behavior of extreme returns. Using extreme value theory, I estimate the statistical distribution of minimal and maximal returns defined as the lowest and highest daily return over a given time-period. Statistical theory states that the asymptotic distribution of extremes has a well-determined form which is independent of the entire process of returns. The extreme value distributions obtained from different distributions of returns are differentiated only by the value of the three parameters of the distribution: the scale and location parameters and the tail index. Especially the tail index indicates the way the tail of the distribution declines. According to the tail weight, three types of extreme value distribution are obtained: Weibull, Gumbel and Fréchet. The Weibull distribution is obtained when the distribution of returns has no tail (we cannot observe any observations beyond a given threshold defined by the end point of the distribution). The Gumbel distribution is reached for thin-tailed distributions such as the Gaussian distribution. Finally, the Fréchet distribution is obtained for fat-tailed distributions of returns such as the Student and stable Paretian distributions.
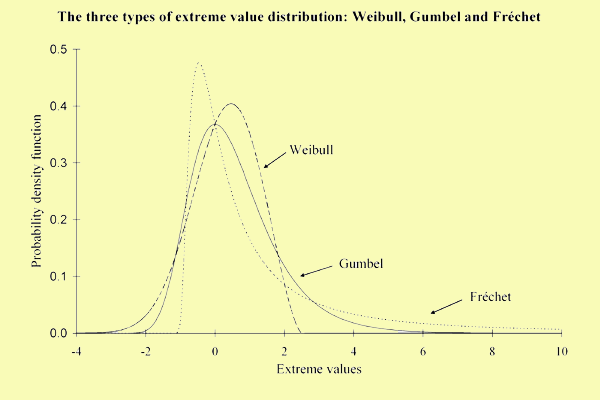
The main empirical finding of this article is that the asymptotic distribution of extremes returns in the US equity market is a Fréchet distribution corresponding to fat-tailed distribution of returns. Moreover, there is little asymmetry between the distributions of the largest declines and the largest rises in the market and the distribution of extremes is fairly stable over time and stable under temporal aggregation.
From VaR to stress testing : the extreme value approach
Extreme correlation in international equity markets
Optimal margin level in futures markets
Retour à la liste des publications
Conseil en gestion des risques
Glossaire de termes financiers
