« Stock market crash » : a magic expression that will definitely attract the attention of every financial investor. Although all market participants would certainly care about such extraordinary events, no research work has ever attempted to give a rigorous quantification of its meaning. Most of theoretical models and empirical studies in finance are interested in the average properties of asset prices such as expected return or expected volatility.
The contribution of this article is to provide some quantitative results on extreme price movements. I apply extreme value theory to financial data. With this statistical framework, extremes in financial markets correspond to minimal and maximal returns defined as the lowest and highest return over a given period. Statistical theory states that the asymptotic distribution of extremes has a well-determined form which is independent of the entire process of returns. The extreme value distributions obtained from different distributions of returns are differentiated only by the value of the three parameters of the distribution: the scale and location parameters and the tail index. Especially the tail index indicates the way the tail of the distribution declines. According to the tail weight, three types of extreme value distribution are obtained: Weibull, Gumbel and Fréchet. Empirically, the Fréchet distribution obtained for fat-tailed distributions of returns seems to fit well the data for the U.S. equity market.
Using the asymptotic distribution of extreme returns, I compute the probability of a stock market crash and its waiting time-period. The waiting time-period represents the average time-period expressed in time units needed to observe a random variable lower (or higher) than a given level. It is a simple and meaning quantification measure.
The table below gives the probability of exceedance and the waiting time-period for the 5th largest extreme price movements observed in the U.S. equity market. An extreme price movement is defined as the lowest daily return observed over one year. The probability of exceedance represents the probability to observe a minimal return over a year lower than the level. The waiting time-period represents the average time-period expressed in years needed to observe a minimal return lower of equal to the given level. Both variables are computed with the extreme value distribution. The database used in the estimation of this distribution consists of daily returns on the S&P 500 index over the period July 1962 - December 1999.
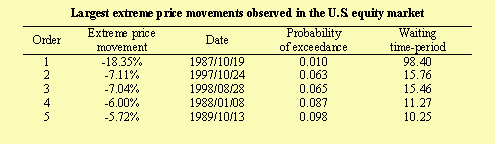
The main result of this research is to quantify extreme events such as stock market crashes. Using the measure of the waiting time-period, the extreme value distribution tells us that a stock market crash like the October 1987 crash would appear on average around every 100 years.
Portfolio insurance and market crashes
From VaR to stress testing : the extreme value approach
Retour à la liste des publications
Conseil en gestion des risques
Glossaire de termes financiers
