

One of the issues in risk management is the choice of the distribution of asset returns. Academics and practitioners have assumed for a long time that the distribution of asset returns is a Gaussian distribution. Such an assumption has been used in many fields of finance : building optimal portfolios, pricing and hedging derivatives, and measuring and managing risks. However, real financial data tend to exhibit extreme price changes such as stock market crashes that seem incompatible with the assumption of normality. For example, the stock market crashes of 1929 and 1987, corresponding to daily market drops of more than 10% and 20% respectively, are very unlikely in a world governed by normality.
Several alternatives have been considered in the academic literature and used with more or less success by practitioners : a mixture of Gaussian distributions, stable Paretian distributions, Student-t distributions and the class of ARCH processes. One problem with these alternatives is that they are not nested and then not directly comparable (by carrying out a likelihood ratio test for example).
The contribution of this paper is to propose a new approach to discriminate among these different models. It focuses on the distribution tails and uses results from extreme value theory. I look at the two extreme parts of the distribution: the left tail and the right tail. The form of the tails is different for the models cited above as the weight of extremes varies. Extreme value theory shows that the tails of most distributions should behave asymptotically in a certain way. It also provides a measure of the importance of extremes in the distribution of returns by quantifying the weights of the tails. This measure called the tail index indicates how the distribution tails decline. Thin-tailed distributions decline as an exponential function and are characterized by a tail index equal to zero; fat-tailed distributions decline as a power function and are characterized by a positive tail index; and bounded distribution are characterized by a negative tail index. The tail index is used to build a formal test to discriminate among the models commonly used in finance.
The table below gives the tail index value for different models of returns commonly used in financial modeling.
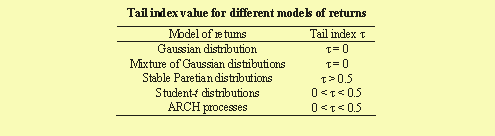
There are several statistical methods proposed in the literature to estimate the tail index from data. Parametric methods assume that a model exactly holds for the tails while non-parametric methods do not assume any particular model as observations are available in a finite number. Using daily returns of the S&P 500 index over the period January 1954 - December 2003, the estimation procedure leads to a tail index estimate, which is positive and likely between 0 and 0.5.
This result leads to the rejection of the Gaussian distribution and the stable Paretian distributions as well. The former contains too few extremes while the later too many. Only the Student-t distribution and the class of ARCH processes are not rejected by the data. This suggests that for the US stock market, a Student-t distribution could be used in an unconditional modeling of returns and that an ARCH process could be used in a conditional modeling of returns.
 The asymptotic distribution of extreme stock market returns
The asymptotic distribution of extreme stock market returns
 From VaR to stress testing : the extreme value approach
From VaR to stress testing : the extreme value approach
 Optimal margin level in futures markets
Optimal margin level in futures markets
 Retour à la liste des publications
Retour à la liste des publications
 Conseil en gestion des risques
Conseil en gestion des risques
 Glossaire de termes financiers
Glossaire de termes financiers