La loi statistique des rentabilités d'actifs joue un rôle important en recherche financière. Des hypothèses concernant le comportement des prix de marché sont nécessaires pour tester les théories d'évaluation de prix et pour calculer la composition des portefeuilles optimaux. Le type de modélisation peut changer les conclusions sur la validité d'un modèle d'évaluation et modifier substantiellement l'allocation optimale des ressources.
Cependant, il n'existe pas de théorie économique ou statistique qui donne la loi exacte des rentabilités. Les lois utilisées dans les recherches théoriques et empiriques sont toujours le résultat d'hypothèses ou d'estimation à partir de données. Au-delà de la loi normale qui constitue le paradigme existant, d'autres modèles ont été proposés avec plus ou moins de succès: les mélanges de lois normales, les lois stables de Pareto-Lévy, les lois de Student, les processus de diffusion avec sauts et les processus ARCH. Le problème rencontré jusqu'à présent est que ces modèles ne sont pas directement comparables entre eux. Comme ces modèles ne sont pas imbriqués les uns dans les autres, un test statistique comme le test de ratio de vraisemblance n'est pas réalisable.
La contribution de cet article est de proposer une méthode pour différencier ces modèles. Ma méthode se concentre sur les valeurs extrêmes contenues dans les queues de distribution et s'appuie sur la théorie des valeurs extrêmes qui mesure de l'importance des extrêmes dans la loi de rentabilités. Cette mesure statistique, appelée indice de queue (« tail index » en anglais), est utilisée pour construire un test formel pour différencier les modèles. Le tableau ci-dessous donne la valeur de l'indice de queue pour les modèles les plus utilisés en finance.
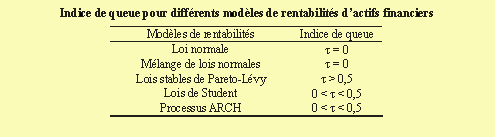
L'article présente aussi des résultats empiriques pour le marché français des actions. Utilisant des données de l'indice CAC Général 240 sur la période 1977-1990, j'estime l'indice de queue. Différentes méthodes sont utilisées : estimation des paramètres de la loi des rentabilités extrêmes définies comme des maxima/minima sur une période donnée ou comme des observations en dessous ou au-dessus d'un certain seuil, et méthodes d'estimation non-paramétriques de l'indice de queue.
Empiriquement, l'indice de queue se situe entre 0 et 0.5. Un tel résultat conduit au rejet de la loi normale et des lois stables de Pareto-Levy. La loi normale contient trop peu d'extrêmes (queues de distribution trop fines) et les lois de Pareto-Levy contiennent trop d'extrêmes (queues de distribution trop épaisses). Les lois de Student et les processus ARCH ne sont pas rejetés par les données. Cela suggère que pour le marché français des actions, une loi de Student peut être utilisée dans un cadre inconditionnel et qu'un processus ARCH peut être utilisé dans un cadre conditionnel.
The asymptotic distribution of extreme stock market returns
From VaR to stress testing : the extreme value approach
Optimal margin level in futures markets
Retour à la liste des publications
Conseil en gestion des risques
Glossaire de termes financiers
