

ARCH processes aim to model the time-varying property of the expected variance of future returns. Such processes capture the persistence of returns in expected volatility: after a small (large) return, the variance is expected to be small (large). However, in ARCH models, the degree of persistence is independent of the size of past returns. This led to the development of threshold ARCH models called TARCH. The threshold effect observed in financial markets means that large shocks are less persistent in volatility than small shocks. In other words, after a big surprise, market volatility increases, but not by much, and comes back quickly to its long-term level. This threshold effect is illustrated in the figure below for the US equity market.
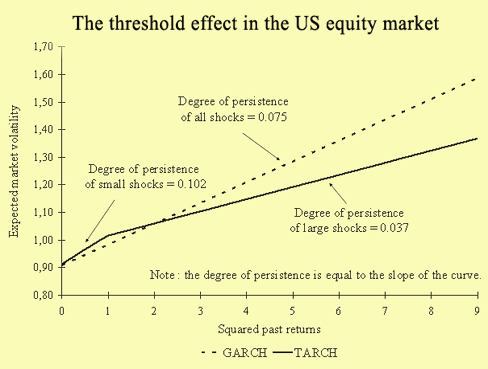
The contribution of this paper is to provide a theoretical model for the threshold effect. The market environment is described as follows: trading for a single risky asset takes place in a centralized market at discrete time-intervals; investors are differentiated according to their motive for trading : liquidity or information. The information process is assumed to be an ARCH process. This reflects the fact that information tends to arrive in waves. A competitive market maker absorbs the net demand for the risky asset at an efficient price. All market participants explicitly take into account the time-varying behavior of the variance of information by computing their expectations and forming their strategies.
It is shown that the variance of market price changes also exhibits a time-varying behavior. When the number of informed traders is exogenous and constant over time, an ARCH process for market price changes is still obtained, but the degree of persistence of the latest informational shock in market variance depends on the number of informed traders. For a given number of informed traders, however, large shocks are as persistent as small shocks. When information is acquired at a cost, and the number of informed traders is endogenously determined, the degree of persistence depends on the size of the shocks : large shocks are less persistent than small shocks. The ARCH process for information is transformed into a TARCH process for market price changes.
 Extreme correlation in international equity markets
Extreme correlation in international equity markets
 The asymptotic distribution of extreme stock market returns
The asymptotic distribution of extreme stock market returns
 From VaR to stress testing : the extreme value approach
From VaR to stress testing : the extreme value approach
 Retour à la liste des publications
Retour à la liste des publications
 Conseil en gestion des risques
Conseil en gestion des risques
 Glossaire de termes financiers
Glossaire de termes financiers