L'approche traditionnelle de la VaR consiste à étudier la loi des variations de valeur d'une position de marché sur une période donnée. Les principales méthodes utilisées pour l'approche traditionnelle que sont la méthode historique, la méthode de simulation de Monte Carlo, et la méthode de variance-covariance sont souvent considérées comme imparfaites. En particulier, ces méthodes ont des difficultés à prendre en compte les événements extrêmes observés sur les marchés, ce qui se traduit par une modélisation des queues de distribution inadaptée. Les événements extrêmes occupent une place centrale en finance et notamment dans le domaine de la gestion des risques financiers. La performance d'une banque sur une période donnée est souvent le fait de quelques journées exceptionnelles, la plupart des journées de trading ne contribuant que marginalement au résultat. De plus, du point de vue du risque systémique, les conditions de crise à l'origine des faillites bancaires intéressent davantage les instances de réglementation que les conditions normales de marché.
La contribution de cet article est de proposer une nouvelle approche pour le calcul de la VaR. Alors que, traditionnellement, l'approche de la VaR consiste à modéliser la distribution de toutes les rentabilités possibles de la position, je ne retiens ici que les rentabilités extrêmes. Utilisant la théorie des valeurs extrêmes, la VaR ainsi calculée utilise les rentabilités extrêmes du marché définies comme la rentabilité la plus élevée (le maximum) et la rentabilité la plus basse (le minimum) observées sur une période donnée. Notons que les rentabilités extrêmes définies dans un sens statistique peuvent être obtenues lors de périodes usuelles correspondant au fonctionnement normal du marché et lors de périodes agitées correspondant aux crises financières. Je considère donc à la fois les petites secousses et les tremblements de terre affectant les marchés financiers.
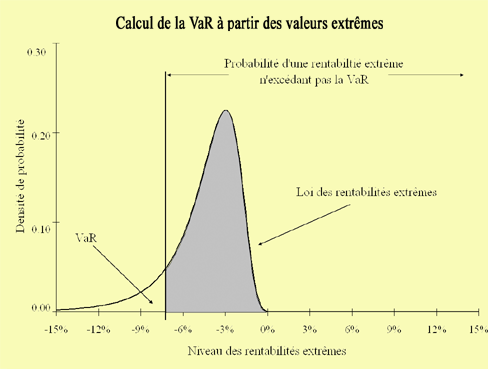
Comme le montre la figure ci-dessus, pour une probabilité donnée, la VaR est obtenue comme le quantile de la loi des rentabilités extrêmes. En pratique, cette loi estimée à partir de données historiques sur longue période est une loi de Fréchet.
Extreme correlation in international equity markets
The asymptotic distribution of extreme stock market returns
From VaR to stress testing : the extreme value approach
Retour à la liste des publications
Conseil en gestion des risques
Glossaire de termes financiers
